圆
基础定义
第一定义
在同一平面内到定点的距离等于定长的点的集合叫做圆(circle)。这个定点叫做圆的圆心。
圆是一个正n边形(n为无限大的正整数),边长无限接近0但永远无法等于0。
第二定义
平面内一动点到两定点的距离之比(或距离的平方之比),等于一个不为1的常数,则此动点的轨迹是圆。
证明:点坐标为(x1,y1)与(x2,y2),动点为(x,y),距离比为k,由两点距离公式。满足方程(x-x1)2+ (y-y1)2= k2×[ (x-x2)2+ (y-y2)2] 当k不为1时,整理得到一个圆的方程。
几何法:假设定点为A,B,动点为P,满足|PA|/|PB| = k(k≠1),过P点作角APB的内、外角平分线,交AB与AB的延长线于C,D两点由角平分线性质,角CPD=90°。由角平分线定理:PA/PB = AC/BC = AD/BD =k,注意到唯一k确定了C和D的位置,C在线段AB内,D在AB延长线上,对于所有的P,P在以CD为直径的圆上。
历史沿革
圆形,是一个看来简单,实际上是十分奇妙的形状。古代人最早是从太阳、阴历十五的月亮得到圆的概念的。在一万八千年前的山顶洞人曾经在兽牙、砾石和石珠上钻孔,那些孔有的就很像圆。到了陶器时代,许多陶器都是圆的。圆的陶器是将泥土放在一个转盘上制成的。当人们开始纺线,又制出了圆形的石纺锤或陶纺锤。古代人还发现搬运圆的木头时滚着走比较省劲。后来他们在搬运重物的时候,就把几段圆木垫在大树、大石头下面滚着走,这样当然比扛着走省劲得多。
约在6000年前,美索不达米亚人,做出了世界上第一个轮子——圆型的木盘。大约在4000多年前,人们将圆的木盘固定在木架下,这就成了最初的车子。
会作圆,但不一定就懂得圆的性质。古代埃及人就认为:圆,是神赐给人的神圣图形。一直到两千多年前我国的墨子(约公元前468-前376年)才给圆下了一个定义:圆,一中同长也。意思是说:圆有一个圆心,圆心到圆周的长都相等。这个定义比希腊数学家欧几里得(约公元前330-前275年)给圆下定义要早100年。
任意一个圆的周长与它直径的比值是一个固定的数,我们把它叫做圆周率,用字母π表示。它是一个无限不循环小数,π=3.1415926535……但在实际运用中一般只取它的近似值,即π≈3.14.如果用C表示圆的周长:C=πd或C=2πr.《周髀算经》上说"周三径一",把圆周率看成3,但是这只是一个近似值。美索不达来亚人在作第一个轮子的时候,也只知道圆周率是3。魏晋时期的刘徽于公元263年给《九章算术》作注时,发现"周三径一"只是圆内接正六边形周长和直径的比值。他创立了割圆术,认为圆内接正多连形边数无限增加时,周长就越逼近圆周长。他算到圆内接正3072边形的圆周率,π= 3927/1250。刘徽把极限的概念运用于解决实际的数学问题之中,这在世界数学史上也是一项重大的成就。祖冲之(公元429-500年)在前人的计算基础上继续推算,求出圆周率在3.1415926与3.1415927之间,是世界上最早的七位小数精确值,他还用两个分数值来表示圆周率:22/7称为约率,355/113称为密率。 在欧洲,直到1000年后的十六世纪,德国人鄂图(公元1573年)和安托尼兹才得到这个数值。如今有了电子计算机,圆周率已经算到了小数点后五万亿位小数了。
相关特点
径
1.连接圆心和圆上的任意一点的线段叫做半径,字母表示为r(radius)
2.通过圆心并且两端都在圆上的线段叫做直径,字母表示为d(diameter)。直径所在的直线是圆的对称轴。
圆的直径 d=2r
弦
1.连接圆上任意两点的线段叫做弦(chord).在同一个圆内最长的弦是直径。直径所在的直线是圆的对称轴,因此,圆的对称轴有无数条。
弧
1.圆上任意两点间的部分叫做圆弧,简称弧(arc)以“⌒”表示。
2.大于半圆的弧称为优弧,小于半圆的弧称为劣弧,所以半圆既不是优弧,也不是劣弧。优弧一般用三个字母表示,劣弧一般用两个字母表示。优弧是所对圆心角大于180度的弧,劣弧是所对圆心角小于180度的弧。
角
1.顶点在圆心上的角叫做圆心角(central angle)。
2. 顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角。圆周角等于相同弧所对的圆心角的一半。
圆周率
圆周长度与圆的直径长度的比值叫做圆周率。它是一个无限不循环小数,通常用字母![]() 表示,
表示,
![]() ≈3.1415926535......计算时通常取近似值3.14。我们可以说圆的周长是直径的π倍,或大约3.14倍,不能直接说圆的周长是直径的3.14倍。
≈3.1415926535......计算时通常取近似值3.14。我们可以说圆的周长是直径的π倍,或大约3.14倍,不能直接说圆的周长是直径的3.14倍。
同心圆
同圆
形
由弦和它所对的一段弧围成的图形叫做弓形。直径一样的圆中,圆的一半小于半圆(周长)。由圆心角的两条半径和圆心角所对应的一段弧围成的图形叫做扇形(sector)。
表示方式
计算公式
圆的周长公式
半圆的周长 c=πr+2r
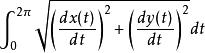 代入,可得
代入,可得
![]()
![]()
![]()
即![]()
圆的面积公式
把圆分成若干等份,可以拼成一个近似的长方形。长方形的宽相当于圆的半径。
圆锥侧面积![]() (l为母线长)
(l为母线长)
弧长角度公式
扇形弧长L=圆心角(弧度制)×R= nπR/180(θ为圆心角)(R为扇形半径)
圆锥底面半径 r=nR/360(r为底面半径)(n为圆心角)
扇形面积公式
R是扇形半径,n是弧所对圆心角度数,π是圆周率,L是扇形对应的弧长。
也可以用扇形所在圆的面积除以360再乘以扇形圆心角的角度n,如下:
(L为弧长,R为扇形半径)
推导过程:S=πr²×L/2πr=LR/2
(L=│α│·R)
位置关系
①P在圆O外,则 PO>r。
②P在圆O上,则 PO=r。
反之亦然。
平面内,点P(x0,y0)与圆(x-a)²+(y-b)²=r²的位置关系判断一般方法是:
②如果(x0-a)²+(y0-b)²=r²,则P在圆上。
③如果(x0-a)²+(y0-b)²>r²,则P在圆外。
②直线和圆有两个公共点,称相交,这条直线叫做圆的割线。AB与⊙O相交,d<r。
③直线和圆有且只有一公共点,称相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点。圆心与切点的连线垂直于切线。AB与⊙O相切,d=r。(d为圆心到直线的距离)
平面内,直线Ax+By+C=0与圆x²+y²+Dx+Ey+F=0的位置关系判断一般方法是:
1.由Ax+By+C=0,可得y=(-C-Ax)/B,(其中B不等于0),代入x²+y²+Dx+Ey+F=0,即成为一个关于x的方程
如果b2-4ac>0,则圆与直线有2个公共点,即圆与直线相交。
如果b2-4ac=0,则圆与直线有1个公共点,即圆与直线相切。
如果b2-4ac<0,则圆与直线有无公共点,即圆与直线相离。
2.如果B=0即直线为Ax+C=0,即x=-C/A,它平行于y轴(或垂直于x轴),将x²+y²+Dx+Ey+F=0化为(x-a)²+(y-b)²=r²,令y=b,求出此时的两个x值x1、x2,并且规定x1<x2,那么:
当x=-C/A<x1或x=-C/A>x2时,直线与圆相离;
当x1<x=-C/A<x2时,直线与圆相交。
设两圆的半径分别为R和r,且R〉r,圆心距为P,则结论:外离P>R+r;外切P=R+r;内含P<R-r;
内切P=R-r;相交R-r<P<R+r。
圆的性质
⑴圆是轴对称图形,其对称轴是任意一条通过圆心的直线。圆也是中心对称图形,其对称中心是圆心。
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的2条弧。
垂径定理的逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的2条弧。
① 在同圆或等圆中,如果两个圆心角,两个圆周角,两组弧,两条弦,两条弦心距中有一组量相等,那么他们所对应的其余各组量都分别相等。
②在同圆或等圆中,相等的弧所对的圆周角等于它所对的圆心角的一半(圆周角与圆心角在弦的同侧)。
圆心角计算公式: θ=(L/2πr)×360°=180°L/πr=L/r(弧度)。
即圆心角的度数等于它所对的弧的度数;圆周角的度数等于它所对的弧的度数的一半。
③ 如果一条弧的长是另一条弧的2倍,那么其所对的圆周角和圆心角是另一条弧的2倍。
①一个三角形有唯一确定的外接圆和内切圆。外接圆圆心是三角形各边垂直平分线的交点,到三角形三个顶点距离相等;
②内切圆的圆心是三角形各内角平分线的交点,到三角形三边距离相等。
③R=2S△÷L(R:内切圆半径,S:三角形面积,L:三角形周长)。
⑤圆O中的弦PQ的中点M,过点M任作两弦AB,CD,弦AC与BD分别交PQ于X,Y,则M为XY之中点。
(4)如果两圆相交,那么连接两圆圆心的线段(直线也可)垂直平分公共弦。
(5)弦切角的度数等于它所夹的弧的度数的一半。
相关定理
切线定理
 垂直于过切点的半径;经过半径的外端点,并且垂直于这条半径的直线,是这个圆的切线。
垂直于过切点的半径;经过半径的外端点,并且垂直于这条半径的直线,是这个圆的切线。
切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线。
切线的性质:
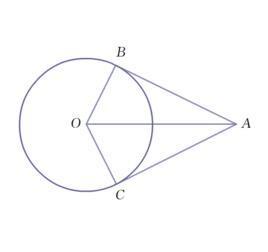
切线长定理
从圆外一点到圆的两条切线的长相等,那点与圆心的连线平分切线的夹角。
以下简述切线长定理的证明。
设OC、OB为圆的两条半径,又∠ABO= ∠ACO=90°
在Rt△ABO和Rt△ACO中
∴Rt△ABO≌ Rt△ACO(H.L)
∴AB=AC,且∠AOB=∠AOC,且∠OAB=∠OAC。
切割线定理
切割线定理的证明:
圆的一条切线与一条割线相交于p点,切线交圆于C点,割线交圆于A B两点 , 则有pC^2=pA·pB
设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT²=PA·PB
证明:连接AT, BT
∵∠PTB=∠PAT(弦切角定理)
∠APT=∠TPB(公共角)
∴△PBT∽△PTA(两角对应相等,两三角形相似)
则PB:PT=PT:AP
即:PT²=PB·PA
割线定理
割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。
一条直线与一条弧线有两个公共点,我们就说这条直线是这条曲线的割线。
与割线有关的定理有:割线定理、切割线定理。常运用于有关于圆的题中。
与切割线定理相似:两条割线交于p点,割线m交圆于A1 B1两点,割线n交圆于A2 B2两点,则pA1·pB1=pA2·pB2。
如图直线ABP和CDP是自点P引的⊙O的两条割线,求证:PA·PB=PC·PD
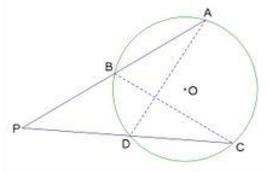
证明:连接AD、BC∵∠A和
∠C都对弧BD
∴由圆周角定理,得 ∠DAP=∠BCP
又∵∠P=∠P
∴△ADP∽△CBP
(如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。)
∴AP:CP=DP:BP
即AP·BP=CP·DP
垂径定理
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧。
设在⊙O中,DC为直径, AB是弦,AB⊥DC于点E,AB、CD交于E,求证:AE=BE,弧AC=弧BC,弧AD= 弧BD
连接OA、OB分别交⊙O于点A、点B
∵OA、OB是⊙O的半径
∴OA=OB
∵AB⊥DC
∴弧AD=弧BD,∠AOC=∠BOC
∴弧AC=弧BC
弦切角定理
弦切角等于对应的圆周角。(弦切角就是切线与弦所夹的角)
求证:∠TCB=1/2∠BOC=∠BAC
∵∠OCB=∠OBC
∴∠OCB=1/2*(180°-∠BOC)
又∵∠BOC=2∠BAC
∴∠OCB=90°-∠BAC
∴∠BAC=90°-∠OCB
又∵∠TCB=90°-∠OCB
∴∠TCB=1/2∠BOC=∠BAC
综上所述:∠TCB=1/2∠BOC=∠BAC
圆的方程
在平面直角坐标系中,以点O(a,b)为圆心,以r为半径的圆的标准方程是(x-a)2+(y-b)2=r2。
特别地,以原点为圆心,半径为r(r>0)的圆的标准方程为x2+y2=r2。
方程x2+y2+Dx+Ey+F=0可变形为(x+D/2)2+(y+E/2)2=(D2+E2-4F)/4.故有:
(1)当D2+E2-4F>0时,方程表示以(-D/2,-E/2)为圆心,以![]() 为半径的圆;
为半径的圆;
(2)当D2+E2-4F=0时,方程表示一个点(-D/2,-E/2);
以点O(a,b)为圆心,以r为半径的圆的参数方程是 x=a+r·cosθ, y=b+r·sinθ, (其中θ为参数)
圆的端点式:
若已知两点A(a1,b1),B(a2,b2),则以线段AB为直径的圆的方程为 (x-a1)(x-a2)+(y-b1)(y-b2)=0
经过圆 x2+y2=r2上一点M(a0,b0)的切线方程为 a0·x+b0·y=r2
在圆(x2+y2=r2)外一点M(a0,b0)引该圆的两条切线,且两切点为A,B,则A,B两点所在直线的方程也为 a0·x+b0·y=r2。
4、圆的三点式方程:过不共线的三点A(x1,y1),B(x2,y2),C(x3,y3)的圆的方程为
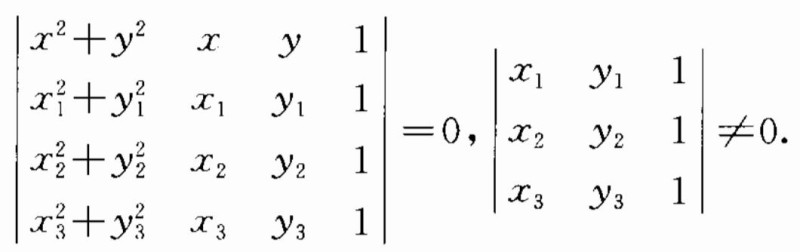
绘制方式
一般情况下可用圆规画出圆形,或用一段绳子,一头固定在地上,一头转,就能转出圆,绳子越长,圆越大。
用AutoCAD绘圆
在AutoCAD“绘图”下拉菜单中,列出了6种“圆”的绘制方法,简述如下:
(1)利用圆心和半径绘圆:用鼠标点取绘图命令,然后根据提示操作;
(2)利用圆心和直径绘圆:用鼠标点取绘图命令,然后根据提示操作;
(3)以两点确定直径绘圆:用鼠标点取绘图命令,然后根据提示操作;
(4)以三点确定直径绘圆:用鼠标点取绘图命令,然后根据提示操作;
(5)以确定半径与两个图形对象相切绘圆:用鼠标点取绘图命令,然后根据提示操作。
richtext控件绘圆
定义一个数组,该数组用来存储一个或多个坐标(Point)
然后按照以下步骤来实现
1 生成一个控件(如Label),并调整相应的属性
2 在内存中建立一张临时的图像作为画布,使用GDI+等各种绘图,将图像绘制到画布上
3 将生成的控件Image或BackGroundImage属性值设定为步骤2生成的图像
4 使用RichTextBox1.Controls.Add方法,将控件添加进去(您可以指定它的坐标)
5 将当前已经添加的控件的坐标记录在数组中(如对应第1个数据)
6 添加RichTextBox1.Scroll事件代码,在该代码中,
 过获取滚动条的值来计算已添加控件应该所在的位置
过获取滚动条的值来计算已添加控件应该所在的位置
说明:控件可以通过代码生成(推荐)
该方法与网上流传的QQ聊天窗口内RichTextBox方法不同,
属于简单型
您务必要定义一个数组,用来参与ScrollBar滚动时,将目标控件重新定位
附件列表
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。

